[알고리즘] 그래프 탐색(BFS, DFS) 기법을 코드로 이해하기

1.그래프

그래프는 광범위한 분야에서 활용되고 있는 자료구조이다. 그러다보니 코딩테스트 문제 출제 1순위이다. 그래프는 정점과 간선의 집합으로 하나의 간선은 두 개의 정점을 연결한다. 그래프는 G=(V, E)로 표현하는데 간선에 방향이 있는 그래프를 방향그래프, 간선에 방향이 없는 그래프를 무방향그래프라고 한다.

V = 정점의 집합, E = 간선의 집합

2.그래프 탐색

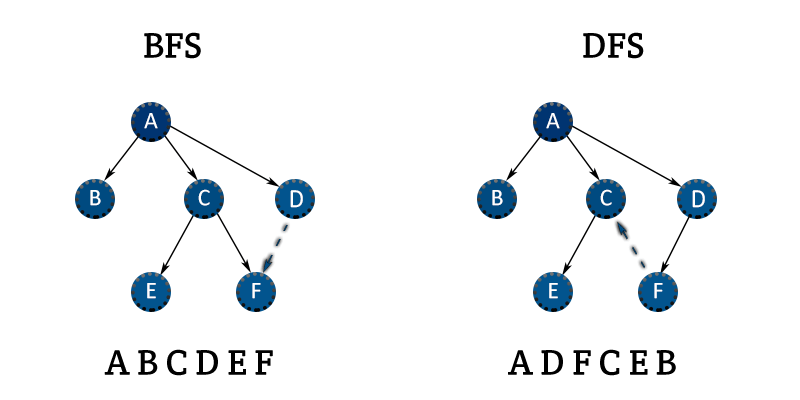
그래프에서는 너비우선탐색(BFS)과 깊이우선탐색(DFS) 방식으로 모든 정점을 방문할 수 있다.

그래프 탐색 예시

2-0.그래프 코드

G = {
	1: set([3, 5])
    2: set([3, 4, 6]),
    3: set([1, 2, 6]),
    4: set([2]),
    5: set([1]),
    6: set([2, 3])
}

2-1.BFS

BFS는 큐를 사용해 임의의 정점(a)에서 시작해 정점(a)의 이웃하는 모든 정점(b)을 방문하고, 방문한 정점들(b)의 이웃 정점들(c)을 모두 방문하는 방식으로 그래프를 탐색한다.

BFS 예시

BFS 코드

from collections import deque

def bfs(graphs, start):
    que = deque([start]) # 탐색중인 큐
	visited = [false for _ in range(len(graphs) + 1) # 방문 여부 확인
    visited[start] = True
    print_list = [] # 방문 순서 저장할 리스트
    
    while que:
    	current_node = que.popleft() # 현재 노드
        print_list.append(current_node) # 순서 저장
        
        for next_node in graphs[current_node]: # 이웃한 노드들 방문
        	if not visited[next_node]: # 방문한 적 없는 노드라면
            	visited[next_node] = True
                que.append(next_node) # 다음에 탐색하기 위해 큐에 넣기
                
	print(" ".join(print_list))

2-2.DFS

DFS는 스택으로 임의의 정점(a)에서 시작하여 이웃하는 하나의 정점(b)을 방문하고, 방문한 정점(b)의 이웃 정점(c)을 방문하며, 더 이상 방문할 정점이 없다면 이전 정점으로 돌아오는 식으로 그래프를 탐색한다.

DFS 예시

DFS 코드

def DFS(graphs, start):
	stack = [start] # 탐색중인 스택
    visited = [false for _ in range(len(graphs) + 1) # 방문 여부 확인
    visited[start] = True
    print_list = [] # 방문 순서 저장할 리스트
    
    while stack:
    	current_node = stack.pop() # 현재 노드
        print_list.append(current_node)
        
        for next_node in graphs[current_node]:
        	if not visited[next_node]:
            	visited[next_node] = True
                stack.extend(graphs[next_node))
    
    print(" ".join(print_list))